Time dilation can be difficult to understand, which is why I’ll dedicate this post to time dilation which is a very real physical phenomena, and not some invention by Einstein. Einstein, and others before him like Lorentz, conceptualized that time wasn’t constant, more so Einstein where Lorentz didn’t fully agree or understand what the mathematics was fully describing. Einstein solidified the concept with his work, which lead experimenters later on to validate his predictions that it existed in the manner he described, without Einstein giving an underlining mechanistic cause, just a superficial geometric description of the effect. Where Einstein’s work stops short (incomplete), my Fractal Scaling Cosmology (FSC) framework explores and explicitly describes a mechanistic cause for time dilation, along with many other things (see https://www.gpofr.com/distortion-time-dilation-experiment/).
What is time dilation? Time dilation is a compensating attenuation on the “normal” passage of time to compensate for the observer’s frame velocity in reference to c, so that the the observer in any frame will always measure c. The velocity of light traveling between different observers, who are themselves traveling at different velocities, travels at a constant c in the same space-time density (quantum medium density as per FSC).
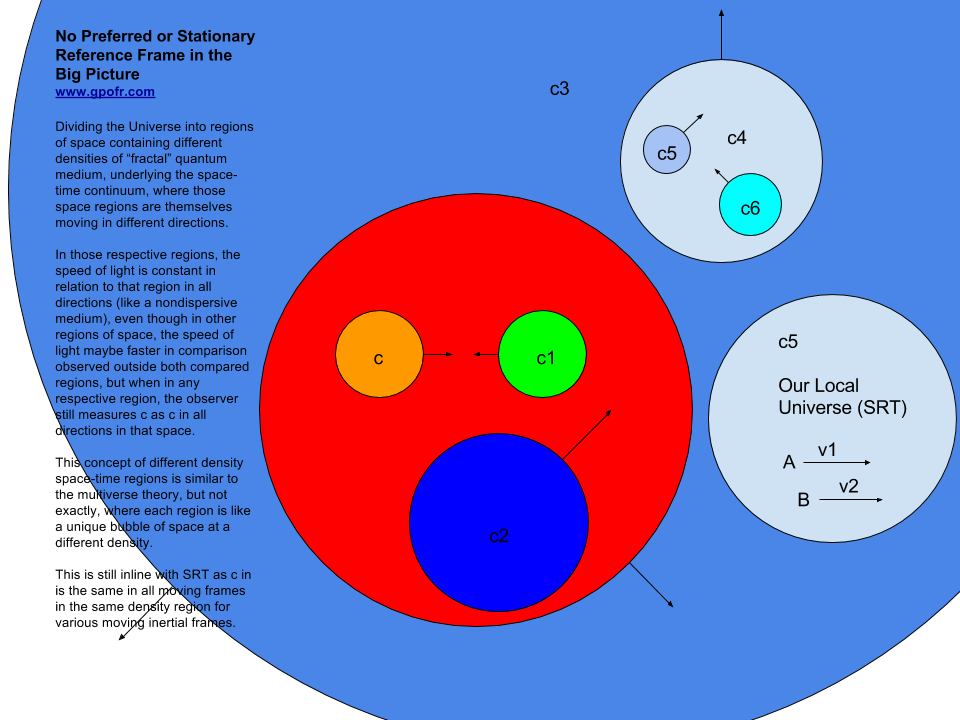
The following diagram is in relation to my own work but touches on SRT and common c in all frames.
I’ll be approaching the topic of time dilation in a slightly different manner mathematically. I personally love a Pythagorean application to derive modified x and t dimensions that mimics the Doppler Effect on the experience of dimension itself. The Pythagorean approach to time dilation gives a view conceptualization of the actual stationary dimension vs. the experienced dimension involved in a simple geometric presentation.
From the Pythagorean diagram above, notice carefully at v = 0 for a stationary observer, c’ = c. This means that our reference to time is through the reference to a constant c, the only true reference. The observer’s velocity doesn’t change the value of c, that is because c in any given space-time quantum medium “material” density (as per my work in FSC) doesn’t change in a non-dispersive medium (source velocity of light source doesn’t add or negate the value of c), and for this to be true along with the observer’s velocity not to affect the measurement of c, that means that the observer’s experience of time must have changed to compensate for his velocity. This doesn’t hold between two different space-time quantum medium “material” densities (as per FSC), but for Special Relativity (SRT) in the same quantum medium density (SRT fits within FSC, as LET fits within SRT). Essentially x’ and t’ are modified versions of x and t dimensions (actually x distance is invariant), and are the versions experienced by a moving observer. Each observer at different velocities in the same space-time quantum medium “material” density will experience different x and t dimensions.
Formulating Pythagorean diagram above:
`c^2 = (x/t)^2 + (c’)^2`
Where c’ is still measured as c within the same frame, because of a modification to x or t dimensions.
`c^2 = (x/t)^2 + ({x’}/{t’})^2`
Since we assume that distance is invariant, therefore x’ doesn’t exist, only x exists.
`c^2 = (x/t)^2 + (x/{t’})^2`
`(x/{t’})^2 = c^2 – (x/t)^2`
`(1/{t’})^2 = (c/x)^2 – (1/t)^2`
`t’ = 1/(sqrt((c/x)^2 – (1/t)^2))`
`{t’}/x = 1/(sqrt((c)^2 – (x/t)^2))`
`{t’}/x = 1/(sqrt(c^2 – v^2))`
`t’ (c/x) = 1/(sqrt(1 – v^2/c^2))` … look familiar?
Since `c/x` derives a time component, since it’s using c and not c’, the time component is considered “proper” time.
`1/t_c = c/x`
`{t’} / t_c = 1/(sqrt(1 – v^2/c^2))`
Finally
`t’ = t_c/(sqrt(1 – v^2/c^2))`
Now how does this visually translate into a scenario of 3 observers measuring the speed of light for a beam of light from their respective inertial frames (in a non-dispersive perfect fluid quantum medium)?
Here c’ is unique to each observer’s velocity in relation to the beam of light, and is derived by:
`c’ = c sqrt(1 – v^2/c^2)`
The calculated value of c’ is still experienced by all observers in their respective velocities as c, and this is because time is experienced differently for each observer in their respective inertial frames due to their respective velocity’s affect on the time dimension.
`t’ = t / sqrt(1 – v^2/c^2)`
So what causes this time dilation mechanistically? From my Fractal Scaling Cosmology (FSC) framework, please read https://www.gpofr.com/distortion-time-dilation-experiment/.
But we’re not finished with SRT. How do the respective observers experience/measure the other observers? This is not a very difficult question to answer. What you have to keep in mind is that the beam of light traveling at c is the common reference in all observer inertial frames.
From Observer A, Observer C is moving away at near the speed of light trailing the beam of light, and Observer C is aging exceptionally slow (clock apparatus moving exceptionally slow in the inertial frame of Observer C). The trailing part is important here. The distance from Observer C and the leading photons in the beam will keep growing because Observer C is traveling at 0.99c. This is good to keep in mind in this scenario.
Now it gets interesting from the perspective of Observer C, and this is where many can get very confused. From Observer C, Observer A appears to be moving away at a velocity close to c, but instead of Observer A aging exceptionally slowly (clock apparatus moving exceptionally slow in the inertial frame of Observer A) from the perspective of Observer C, Observer A is actually aging exceptionally fast yet moving away from Observer C also exceptionally fast. This might appear to contradict SRT at first, but it really doesn’t, because in relation to the beam of light traveling through the space-time medium, through all three inertial frames for each observer, it is Observer C who is actually traveling near the speed of the beam of light, and not Observer A. This becomes even more emphasized when you consider that the space-time medium is a non-dispersive medium, where the source velocity of light does not affect the velocity of the photons (as per FSC), meaning it doesn’t matter which inertial frame is emitting the beam of light (as per SRT). It is very important to cautiously remember, and fully understand, that the beam is common to all frames. Also the distance from Observer A and the beam source will essentially stay the same from the perspective of Observer C in this scenario depicted in the diagram above.
Again from my work in Fractal Scaling Cosmology Framework (FSC), the following diagram depicts that in different space-time quantum medium “material” densities, each respective region has its own value for c, yet each observer will still experience the normal value of c in each respective region because of the medium’s density affect the dimensions distance and time, but not across two different regions. Between two different space-time quantum medium densities, light will experience refraction.